Step 1
For the first three steps we don't care about the U or D layers. So whenever you have to turn an inner layer, you can turn the outer layer along side it. That should speed things up.

Solve the upper inner corners.

To move the final corner from the lower layer to the upper layer, position at the front right and use the algorithm R d' R d R. It sounds like a pirate laughing, har-de'har-de-har!!
Step 2

Solve the bottom corners.

I usually turn the puzzle upside down to swap corners. To swap the two facing you use the algorithm F u L F u F u' R u F.
Step 3

Solve the inner centres.

I do this by using the algorithm u2 R u2 R u2 R which swaps the front upper centre with the one opposite it at the back.
To move them between layers I wrap the algorithm in a setup move. So doing F before and after swaps the bottom front with the top back.
Another common setup move variation is swapping the top front centre with the top right centre.
Really I just make up the variations as I go.
Step 4


Do the first three steps again with the outer layers, and (u, d) changed to (U, D) in the algorithms.
Bottom right corner to top right to solve the top corners:
Flip the two top front corners:
Swap the top front edge and the back top edge:
Be sure not to split up the centre slices because, although they will get mixed, the two layers will always match each other.
Step 5
The previous step messes up the positions of the centre layers. It's pretty easy to counteract. I use some extra notation here, C is u and d' together, in other words, move the two central layers one quarter-turn clockwise when looking from above. M is a half turn of the central slice (containing the top and bottom centres and the two centres on the front layer).
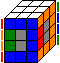
The algorithm which rotates these three edges is C L C L C2. You can usually achieve a lot by spamming this algorithm.
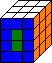
If you need to swap the two front centres with the two back centres do M d2 M d2.
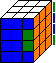
Here is the dreaded parity case. The algorithm to sort this is d2 R u M d2 M u' R d2.
The end